Just outside my window, in an AirBnB in Ghent, there is a tree with character. It leans in towards the window as if it wants to say something to me. This talkative tree made me think back to a debate in the Dialogic Education conference in New Zealand in 2014 when Alexander Sidorkin – Sasha – argued strongly that you could not have a dialogue with a tree. People who talked of dialogue were just projecting their own thoughts into the tree, he said. For Sasha this claim had significance for education as it also applied to other situations where dialogue was claimed but there was no real reciprocity. Very young children for example or those with specific learning difficulties of a type that might prevent true dialogue.

​Figure 1: the tree that started this blog


Perhaps the tree was mentioned because Buber, sometimes cited as one of the thinkers behind dialogic education, mentioned a kind of dialogue with a tree in his classic text ‘I and Thou’. His main argument in ‘I and thou’ (Ich und Du) is that how we orient ourselves to others makes a difference to how we see them or feel them. We can objectify them, turn them into things to be studied and classified, - the ‘I to it’ orientation - or we can relate to them in a responsive way as others who also make meaning – ‘the I -thou’ orientation. The key indication of the ‘I-thou’ orientation is that we are open to the possibility that we might learn something.

It is sometimes forgotten that Buber’s argument was not just about how we treat other human beings but also about how we relate to otherness in general including how we relate to God and how we relate to nature. Early in the book, to present his main thesis that how we orient to others matters, he gives the illustration of how we can relate in different ways to a tree: we can see it aesthetically, as lines and colours, standing back from it as if was a picture, we can relate to it as just  an instance of universal scientific laws or we could perhaps dissolve it into numbers, the measurements, the number of carbon atoms etc. These are all examples of variations of an objectifying ‘I to It’ orientation. Buber continues that it is also possible to take a different orientation to the tree and relate to it as a thou.

Figure 2 Buber

Buber uses the term ‘reciprocity’ implying that he means a dialogic relation. This raises a challenge for how we understand the essential dialogic relationship that underlies theories of dialogic education. Dialogue is often defined as requiring two or more subjectivities each actively orienting towards the other or others in the dialogue. It seems unlikely that the tree outside my window really has a sense of my existence and is orienting itself towards me. But I think that there is another way of defining the essential dialogic relationship.

Here is my alternative definition:

In a dialogic relationship there are two sides, an inside and an outside, held in a relationship of tension in which they can reverse perspectives but not join.
​
For example, let us assume that I am talking to you now as I write. My own thoughts are open to me as if they are in field of light. I can see my intentions as I plan my next sentence. My intention is to reach you, to make you stop and think, so I really have you in mind all the time. But your thoughts are dark to me. The dialogue, this dialogue here, has two sides, an inside – ‘me’ – and an outside ‘you’. But the outside is not bounded – I do not even know your name – you could be anybody and probably are. Just imagine if this blog somehow survives the destruction of the earth by asteroids in the next century and is found by aliens in a structured fragment of computer hard-drive floating in space in a million years’ time. Perhaps that is ‘you’?

Figure 2: A possible reader?

Nonetheless, despite the unknown nature of my interlocutor, I sense that there is a dialogue. To write I need to take your position and imagine your response. More than this, the writing – my ‘voice’ which I hear in my head even as I type rapidly on the keyboard – emerges out of the relationship between me and you and would not be possible without that tension. I am not writing just what I think nor just what I think you want to hear but something in-between – something that would not exist or make sense without both sides in the dialogue.
 
Dialogue as ‘superposition’

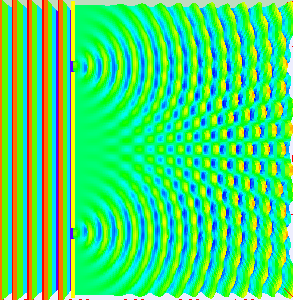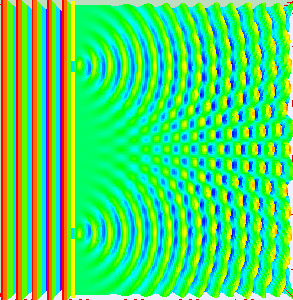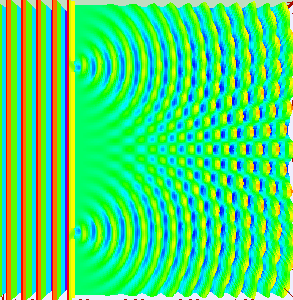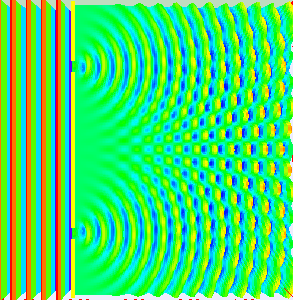
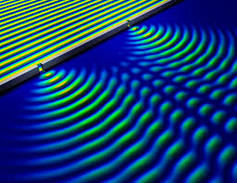
One barrier to understanding Buber’s position on dialogue with a tree might be some everyday assumptions about the physical world. According to everyday physics, the physics of Newton still taught as ‘true’ in schools, there is a box of space and time containing physical individuals and two different physical individual bodies cannot be in the same place at the same time. The everyday image of dialogue assumes this everyday physical world in which different people, incarnated in bodies, talk to each other through brains that form sentences and mouths that speak them. Trees do not have brains and mouths so it seems unlikely that they have a voice. The rather more modern – if already one hundred years old now - quantum theory of the physical offers a very different image. This is ‘superposition’ or the claim that while we do not know what the state of any object is, it is actually in all possible states simultaneously, as long as we don't look to check. It is the measurement itself that causes the object to be limited to a single possibility. Wave-particle duality is a good example easy to demonstrate in the classroom. This is the claim that light is both a wave and a large number of small particles at one and the same time. As a wave it acts as a collective and as particles it is made up of many separate individual paths. (see figure 3) Whether light appears as a particle or as a wave depends upon how we set up the experimental apparatus to observe it. 

As Karan Barad brings out (see previous blog) issues of superposition and quantum entanglement cannot be contained to the lab. Although wave-particle dualism is presented as if it refers only to light in a small space really superposition involves the whole universe. Each electron exists only as a potentiality of the universe until it is observed. [See Brian Cox on the ‘everything is connected to everything else’ consequence of quantum theory on https://youtu.be/ASZWediSfTU] According to Barad reality for us with its space and time and its subjects and objects is always to be understood as a kind of crystallisation (collapse of the wave function) to form a particular configuration of the world out of a state of potentiality containing all the other possible configurations. Each crystallisation of a particular configuration of reality represents the forming of an inside (our experience)  in relation to an outside (the invisible context). Through quantum theory it is clear that the invisible context is not an elsewhere that has no impact on our experience but is intimately bound up with the visible experienced world and in a sense is to be thought of as its inside (‘in-forming’ it) as well as to be thought of as on it is outside something over there in the distance that we do not need to take into consideration.
 
I not aware if Buber knew much about quantum theory but one implication of his main thesis is that when we observe the world in ‘I-it’ mode we fix a world of distinct objects and when we observe in ‘I-thou’ mode we open up a very different world of entangled relationships and possibilities of learning across apparent boundaries.
 
By taking an I-thou attitude we are opening up the gap that separates a person  from a tree in a way that opens up something else - the potentiality for different ways of being that underlies that gap. This is not a way of accessing the secret intimate thoughts of the tree itself but perhaps we are accessing the entangled quantum state that underlies the division me/tree. This space is not empty. The quantum world is not indivisible, as Buber suggests it is in the quote above, but has a topology with many structural features particularly probability curves suggesting where particles are most likely to occur.
 
If the ‘I-thou’ mode involves an element of stepping back into that quantum state then through this move I can, intuitively, find myself on both sides, both inside and outside, both observer and observed[i].
 
So was Sasha right to claim that I am just projecting my feelings into the tree when I dialogue with it? Yes and no. It is perhaps true that dialogue with nature can be a way to dialogue with what Freud and Jung call the unconscious mind. Feelings that we have but do not acknowledge might be recognised when projected outside us into nature. But in exactly the same way we could talk of the tree projecting its thoughts into me. The point is that neither I nor the tree are the primary reality here, the primary reality that thinks and talks and sees, is an entangled system including the potentiality to be me and to be the tree. If you hang around long enough with trees you will find yourself having tree-like thoughts that well-up as if from the inside. The nervure of the leave is already a model for many areas of thought (see figure 4 - leaf). More poetically the mood of this tree, its dark warm stillness surrounded by the green fluttering energy of its leaves – perhaps reaches me from the inside.

 

​The idea here of ‘dialogue’ with a tree is of how an entangled unity of me and the other can issue in a hybrid creative thinking. When new ideas come it is not always obvious that they come from inside me and not from outside me. Wittgenstein once wrote in his diary that when he was really thinking then everything he came across became for him a model of the problem he was thinking about. Similarly Nietzsche wrote of his inspiration ‘it is as if the things themselves approached and offered themselves as metaphors’.
 
Technology
The focus here on dialogue with a tree might suggest some sort of ecological movement in education engaging more with nature. There is evidence that there can be a positive impact on wellbeing from time spent with trees and with nature. But the argument in this blog applies just as much to the technological environment – a kind of second nature - of young people today. Entanglement with nature can help understand the identification with places of many cultures, perhaps most strongly, Australian aboriginal groups. It can also help us understand how a new identity might form entangled with the global or unbounded community interacting on many Internet spaces.

Educational implications
In school, in the context of reading poetry, I recall being told, in no uncertain terms, that projecting feelings onto nature was a fallacy, not just any fallacy but ‘the pathetic fallacy’. Nature did not have feelings, the teacher said, only humans can have feelings – the world is quite neutral but humans project meanings and emotions onto it.

Vygotsky was simply articulating the dominant view of his time when he wrote, in the 1920’s, that the children’s thinking is ‘participatory’, a style of thinking that children share, he claimed, with primitive people and with schizophrenics, (Vygotsky, 1986, Thought and Language, p 236). His aim, again just voicing the assumptions of his time, appeared to be education out of participation and into more abstract more logical ‘scientific’ thinking. The same view is even clearer in Piaget. The implications of dialogue with trees and all forms of non-human otherness is that participation is not just a starting point of education to be trained out of children, but is essential. It is the source of meaning. The perpetually renewed source of science as well as of art. It is also, not insignificantly, the perpetually renewed source of faith that life is worth living.
​
There are pedagogical issues to be addressed about how to teach and learn subjects like maths, science and literacy in ways that do not cut the umbilical cord with participatory meaning. I have referred to this elsewhere as teaching which deconstructs with one hand while it constructs with the other. Basically we can construct selves and ‘knowledge’ and ways of thinking that are light and open, porous to the outside, always aware of their provisional status and so able to change.

But as well as the pedagogical issues there is perhaps a more important issue here to do with meaning. If there is a larger thinking that thinks us as it thinks the trees and the stars, then meaning comes from our participation in that larger thinking. Meaning therefore requires surrender as much as it requires construction. It turns out that traditional religious world views have been right all along in certain fundamental respects and modern secular humanist rationalist world views, dynamic as they may have been, have missed out something rather important.  If only those clever people peddling the view that the universe is meaningless had spent more time as children in dialogue with trees. As Buber almost said, once you have had a proper dialogue with a tree it becomes no longer possible to find the universe meaningless. So perhaps having a dialogue with a tree is another one of those basic  ‘skills’ that ought to be on the curriculum.

​[i] This appeal to quantum theory is speculative. It is inspired by Hameroff and Penrose’s understanding of the quantum basis of experience illustrated here:

​(Picture from Hameroff Stuart; Penrose Roger
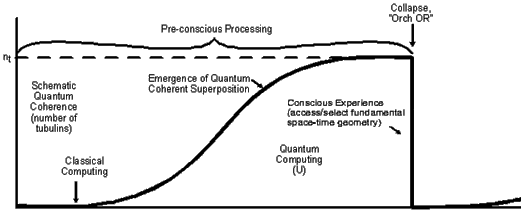
Consciousness in the universe: A review of the 'Orch OR' theory.
Phys Life Rev, 2014; Mar 11(1):39-78.) Other arguments could be made. We could look at how the image of the tree and image of the self are stored in an entangled way in the brain. ‘Seeing’ the tree involves a kind of holographic projection from the brain (https://youtu.be/3MSw2irv0-A) implying that in a sense I (as my brain before projection) am also already the tree that I see. The ‘real’ tree and the ‘real’ me that is interacted with in order to produce the holographic projection that we call perception would have to be described in quantum level terms. Merleau-Ponty does a phenomenological reduction to explore how clear images such as trees and bodies (ie me) emerge from a much less clear ‘pre-thematic’ perceptual ground. This pre-thematic field of potential perception precedes and exceeds actual perceptions. In other words the argument about being both inside and outside acts of perception does not depend entirely on the appeal to quantum theory.
 

1.The idea of crossing disciplinary boundaries
​
A few years ago, in a research team meeting for an education project, I raised the issue of reflection in learning and Lindsay Hetherington, a lecturer in science education, commented that Karen Barad – a feminist philosopher and quantum theorist - criticised the metaphor of reflection preferring the more complex metaphor of diffraction. That evening I looked up Barad up on the internet, watched a You Tube video, became interested and bought her book ‘Meeting the Universe Halfway’ via Amazon. Now I am trying to apply her ideas to education. Did Lindsay have agency there in causing my learning? Was she my teacher? Does it matter to your answer if Lindsay had the intention to teach me or not?  Barad argues that agency is not an attribute of people: ‘.. agency is a matter of intra-acting; it is an enactment, not something that someone or something has. It cannot be designated as an attribute of subjects or objects (as they do not pre-exist as such).’ And indeed it is true that it is only after I observe the event of learning – my learning about Barad’s quantum-physics based philosophy in this case - that I can go back and trace its causation and try to attribute agency. That agency is distributed and complex including You Tube, the Internet and the material book that I bought and also perhaps the larger systems (my job, my background in the current political economy etc) that enabled me to read it and have time to think about it.

 Quantum theory describes the behaviour of sub-atomic particles so it might seem quite a stretch to apply this to education. At best such a move might be seen as loosely metaphorical in the way that people often mention wave-particle duality when they really just want to say that two different ways of looking at things both seem to have some truth in them. At worst it could be seen as a gesture towards the sort of scientific reductionism that claims that to really understand anything we need explanations in terms of the underlying physics. But I find that quantum theory helps me understand what is going on in education and this is neither as a metaphor nor as a reduction to the physical. So let me try to explain why I think that quantum theory matters.
 
First I have to acknowledge that I cannot read quantum theory in its proper mathematical language but only after translation into my kind of ordinary language. While I can appreciate some of the elegance and significance of Schrodinger’s famous wave function – the most iconic representation of quantum theory –it speaks to me mainly as something mysterious and exotic, like an artefact from an alien civilisation.
 

However, once translated into prose, this formula and others seem to describe the physical world better than any other theory available in a way that implies a suspension of belief in common-sense views of time, space, causality and identity. In place of common sense we have a completely new way of thinking involving superposition, quantum entanglement, and non-local causation.
 
Looking at dialogues in education has led me to propose that, to understand processes of dialogic learning, we need to switch from a (monologic) ontology of identity – the idea that there are separate things such as people and words that interact – to a (dialogic) ontology of difference  – the idea that differences are more fundamental than identities and constitutive of identities[i]. However, I find the idea that relationships come first, even before the things that are supposedly in relationship, is difficult to think through and certainly difficult to articulate clearly and persuasively. I mean it does not really make much sense to claim that my relationship with you in this moment (hi) is what makes you to be you and me to be me as if we did not exist before the meeting (– or does it? Who are you in this moment? When exactly did you come into existence and in what form?). Common sense thinking says that there is me sitting here in my chair and you, at some distance away, over there, reading these words that carry messages between us, messages which might cause changes in us over time depending on how we respond to them. So what fascinates me most about quantum theory is that it is a systematic and rigorous thinking through of the implications of a difference ontology in a way that is not merely of creative interest but really seems to work to help us understand reality.
 
It is true that theory in the field of education does not need to conform to theory in field of sub-atomic physics. However, fundamental assumptions such as the idea that meaning can be grounded on describing interactions between definable things (atoms, people, words etc) or that events are caused by physically local mechanisms (the ‘principle of locality’) are general assumptions that are not specific either to physics or to education. If one area – sub-atomic physics – has generated a set of new assumptions that work better to explain how the world works then that new way of thinking can spread to other areas by a process of transduction. Anyway, the assumptions that seem so basic to common sense and even appear to be embedded in the way we have to use language in order to communicate with each other, turn out, on closer philological examination, to be the residue of now superseded physical theories (atomism, local causation, absolute space-time etc). If our fundamental assumptions about reality originate in a physical world view we now know to be false it is reasonable to challenge their application to education by seeing what happens if we replace them with ideas that are slightly more up to date although already tried and tested over about a 100 years..

2.Dialogue and the central paradox of education

What many take to be the central problem for educational theory was outlined by Meno and re-stated by Socrates in a dialogue written down by Plato:
"[A] man cannot search either for what he knows or for what he does not know[.] He cannot search for what he knows--since he knows it, there is no need to search--nor for what he does not know, for he does not know what to look for.”[ii]

This problem has been addressed in various ways by Piaget, Vygotsky, Bandura and others. All the solutions assume the separate identity of a learner facing a world and account for how changes in the identity of the learner are caused in an essentially mechanical way by internal and external processes. Quantum theory, by questioning the assumption of separate identity at the heart of the paradox, perhaps suggests the possibility of a different approach to educational theory and so a different approach to education..
 
Dialogue has been put forward as one response to Meno’s paradox of how people can know things that they do not yet know. Vygotsky suggested that learners go through a ‘zone of proximal development’ where relationship with a teacher (or more able other) enables them to do things, and understand things, that they could not do or understand alone and unaided. I have tried to augment this account with the simple idea that in dialogue you do not just learn by internalising the other’s point of view but, more importantly, you also open up a dialogic space in which many (ultimately an infinite number) of points of view play. [see my earlier blog on dialogic space] Notice that this view shifts the focus from dialogues as people exchanging words in physical space-time to a more meta-physical or poetic sounding  idea that the gap between people in dialogue has a certain reality.

 
But what exactly is the status of this ‘dialogic space’ and what exactly are the mechanisms for the learning that occurs in dialogue? Sometimes a kind of focussed collective learning occurs through dialogue which is neither about each taking on board the already formed ideas of the other nor the random effervescence of multiple new ideas that might perhaps be assumed to arise from opening up a new space of possibilities.  Merleau-Ponty described this[iii]:

​Merleau-Ponty is concerned with the issue of how the ‘truth’ (relative to a context) emerges and gains acceptance. His point here is that sometimes we find ourselves saying things that seem to want to be said.
 
Freeman Dyson, who made a major contribution to quantum theory, claimed to experience new ideas flowing through him. As Merleau-Ponty describes how his words seem to go ahead of his conscious understanding so Dyson, who is writing, ascribes this agency to his fingers:
 
“I always find that when I am writing, it is really the fingers that are doing it and not the brain. Somehow the writing takes charge. And the same thing happens of course with equations .. The trick is to start from both ends and to meet in the middle, which is essentially like building a bridge.”[iv]
 
Freeman Dyson found his fingers leading him on the journey of what wanted to be said even though he did not know yet what that was. It was as if the ‘truth’ (the best representation in the context) here followed him and he only recognised it after the event. I think that this is quite a common experience. It is even something that I have observed researching children solving reasoning test problems together. The more the dialogic space opens the more solutions to problems seem to emerge spontaneously. Habermas wrote, in this context, of the ‘unforced force of the best argument’ emerging out of free and fair competition between multiple ideas. But this is not how it happens. Talk and explicit reasoning are important only after the event of creativity in which a new solution emerges often fully formed or nearly fully formed. Talk and explicit reasoning of the kind defined by Barnes and Mercer as ‘exploratory talk’ are useful for sharing insights and for checking them to see if they solve the problem but this talk does not have much role in directly generating creative insights in the first place.

​​3. Why a neuro explanation is not enough

One direction to go in understanding the learning ahead of oneself effect or how we often already seem to know more than we could possibly know, is through the phenomenon of incubation studied by neuro science.
 
Detailed experiments into the ‘aha’ effect described by Kounios and Beeman demonstrate that the brains of participants can be observed to solve problems before the participants themselves are aware of this and so the solutions ‘pop’ into consciousness as if from outside them.  This is an interesting area of research which I have described elsewhere (Wegerif, 2012, p64). However one important limitation with much supposed neuro-educational explanation is that it assumes a pre-quantum theory mechanical world-view. The assumption seems to be that thought has a material instantiation in neuronal processes that can be completely described in terms of classical mechanics. Creativity, it is claimed, forms in time within individual brains where neurons interact according to traditional mechanisms of local causation. There is an old philosophical objection to this which is neatly expressed by the point that the world is in the brain as much as the brain is in the world. But now that we are building quantum computers relying on superposition effects and quantum level effects have been found to be central to understanding even such basic biological processes as photosynthesis [https://youtu.be/_RSKI5A_lsg]  it is beginning to seem unlikely that something as complex as thought has no quantum level aspect. (See Penrose, R Emperor's New Mind and https://youtu.be/3WXTX0IUaOg] ) 
​

​4.Applying quantum theory

Karan Barad, a philosopher who is also a quantum physics researcher, is, I find, a reasonably careful and persuasive guide to some of the implications of applying quantum theory to our experience of reality beyond the physics laboratory.

  Step 1: Barad begins with an account of how the apparatus used to measure or observe matter can be shown to determine whether matter appears in wave from or particle form and even determine in advance the paths that photons choose to take as if they could predict the upcoming observation [see e.g https://en.wikipedia.org/wiki/Wheeler%27s_delayed_choice_experiment].

It follows from these experiments, as Bohr argued, that any description of matter needs to include a description of the apparatus of measurement. To restate this: ontologically it is not possible to separate object from subject. Both are together in one system, called an apparatus. The exact boundaries and nature of the object and the subject depend upon the way in which the measurement is made – the ‘agential cut’ as Barad calls this. Since the apparatus is a machine for producing space and time it cannot be thought of as located within space and time.

 Step 2: She argues that the apparatus has no clear boundaries. ‘Is the printer attached to the computer part of the apparatus?’ She asks and continues ‘How about the community of scientists who judge the significance of the experiment and indicate their support of lack of support for future funding?’. If the configuration of matter observed by the apparatus is called the phenomenon then each apparatus is itself an observed phenomenon for a larger apparatus. (2007 P143 p161)

 Step 3: It follows that reality is made up of phenomena produced by apparatuses which are themselves also phenomena. Subjects and objects are entangled together in a single system that, as a result of each ‘agential cut’ (an observation leading to a collapse of the wave function) separate out such that a subject looks at an object. In reality this could be thought of as just one thing looking at itself which is why Barad replaces the term inter-action between observer and observed with the term ‘intra-action’. This is a relational ontology in which ‘relata only exist within phenomena as a result of specific intra-actions (i.e there are no independent relata, only relations within relations).’ P429

Socrates’ solution to the educational paradox introduced by Meno (above) was that learning new things is actually a kind of recollection. We have access to an eternal soul that knows everything but when we incarnate we forget and the role of the teacher is to help us remember.

Barad’s version of Bohr’s interpretation of quantum could perhaps be read as offering a solution which is similar. Who we think we are – finite beings often closely identified with our physical bodies - is a kind of forgetting produced by an ‘agential cut’ (the collapse of the wave function). Who we really are is the whole entangled system before the cut including material objects and other people. Educational enquiry is not therefore, on this reading, about constructing new knowledge from scratch so much as about deconstructing the gap that separates us from who we really are and so from what we already know intuitively.

But Barad is not saying that. For her there is no true ‘self’ or true ‘thing’ underlying phenomena as there are no separate things at all, only one dynamic process. This means that ‘God’ or ‘the Universe’ should not be thought of as some sort of underlying agent. As she puts it: ‘Agency is not an attribute but the ongoing reconfigurings of the world. The universe is agential intra-activity in its becoming’.  The educational implication is not that we retreat passively to a state of mystical union before the cut but that we participate more wholeheartedly in the creativity of the universe which consists of making new cuts, configuring and reconfiguring the world in new ways. Ethics and responsibility is bound up with the realisation that we are, in a sense, all the others and all the possibilities of matter.
 
5.And dialogic education?
​
Barad’s theory of agential realism fits in some ways with insights from dialogic theory but is useful in extending dialogic beyond culture to incorporate the material world.  We do not just dialogically construct meanings, we dialogically construct matter. But what we mean by ‘we’ here has to extend to include the material world. Let me explain.

The standard model of agency that Barad is aiming at replacing is that of an autonomous self with intentions that get realised in acting on the world. A dialogic account of agency is already not like that. Let me illustrate this with a little made up story.  I have a dialogue with some friends about whether to eat Indian, Chinese or Italian food tonight. I start off wanting Indian but we end up eating Italian. I could experience that as my agency being overridden by the others, or, maybe I listened and found myself persuaded that Italian would be better. This can happen partly because the fact that someone else wants something often makes it seem more desirable to me. In dialogues there is a participation in embodied feelings as well as in abstract ideas and salivating over the prospect of a good pizza is an embodied feeling that can be transmitted. On the way to the Italian restaurant we find the road blocked by barriers around a fallen tree and so we turn to try to find a way around. In the process we come across a gastro pub with a special offer and a great aroma. We all agree that this is the best option and feel grateful that the tree falling led us to make a new discovery. This little story is meant to illustrate Barad’s idea of entangled agency that is realised only in enactment. Lots of voices enter into the final outcome in a way that is not separable and includes physical objects such as a fallen tree. But this is precisely the nature of dialogic agency. When we make decisions and act through dialogue I find that I can participate – I sometimes lead and sometimes follow - but I cannot control. When the dialogue is working I identify with it and take joint responsibility. The fallen tree begins as a barrier to our intentions but ends as a contributor to a new beginning.
 
Entanglements produce what Simondon called ‘trans-individual’ effects or the agency of larger wholes. This explains Freeman Dyson’s feeling that his fingers led him to express truths about quantum physics before he had understood them himself. He became entangled with the literature in the area which is also to say that he became entangled with the behaviour of sub-atomic particles.  He was on both sides at once building a bridge - as he put it. His new theories were not his alone, nor were they the voice of the universe simply possessing him in order to explain itself to itself  - the agency was entangled and enacted. This explains the paradox of educational dialogue and inquiry, that we can learn new things and become new people and create new worlds in the process.
 
The boundary between me and you in a dialogue is constitutive of the dialogue – there is no dialogue without the boundary. I have focussed a lot on that boundary in the past. But Barad reminds us that there is also a boundary with the matter of the dialogue, with what we talk about.  And the tools we use to support the dialogue enter in as agentive voices in their own right, I mean, for example, the particular concept words or other technologies such as computer software. If we pause and question these boundaries and open them up into a space of possibilities and enter into that space then we are truly in dialogue. Being able to cross-over and see things from your point of view as well as my point of view is only possible because we share a ‘prior’ or ‘underlying’ space of possibilities. Similarly Freeman Dyson being able to cross over and see things from the sub-atomic particles’ point of view was also only possible because of a shared space. Einstein writes about how he formed his theories out of a kind of dialogue with the universe in which he imaginatively role-played being a beam of light and such-like. Dialogue is possible because we are not completely contained by the configured world that we experience on the collapse of the wave function.  The space that opens up in dialogue – dialogic space -  is a return – always partial – to the space of all the  possible perspectives and meanings before the cut was made and a particular reality became crystallised. The words we use in dialogue and the many little thought experiments we use are themselves ways of reconfiguring the world in order to creatively explore its possibilities.
 
Applying quantum theory to education helps us to understand how dialogues can work by unpicking boundaries, opening a space of potential and allowing learners to respond to the call of flows of meaning that originate beyond them and behind them. These flows of meaning can take the form of long-term cultural dialogues – like the long-term dialogue of Mathematics mentioned in my last blog. But culture is always entangled with matter and with nature. Barad’s account of the emergent and dynamic agency that arises from quantum entanglement – agency that we participate in but do not control -  perhaps also explains a flow of meaning many feel called by that seems larger than culture – as if the universe itself was seeking to know itself and to love itself through us.
 

​​Barad, K. (2007). Meeting the universe halfway: Quantum physics and the entanglement of matter and meaning. duke university Press.


[i] Wegerif, R (2008) Dialogic or Dialectic? The significance of ontological assumptions in research on Educational Dialogue. British Educational Research Journal 34(3), 347-361.]
 

[ii] .Plato, Meno, 80e, Grube translation.

[iii] Merleau-Ponty, M (1968) The visible and the invisible. Northwestern University Press.

[iv] Quoted in Csikszentmihalyi, M. (1996). Creativity: flow and the psychology of discovery and invention. New
York: Harper Perennial.

In writing this blog I was also thinking of (in dialogue with?) David Bohm's work on realist quantum theory and on dialogue, about Deleuze's work especially 'immanence: a life'  and, of course, about Spinoza - 'the Christ of Philosophers' as Deleuze calls him.

Leonard Cohen was once asked by an interviewer why he had moved into pop music after making a career as a serious poet. He said ‘I thought that I would get more girls’. ‘and did it work?’ responded the Interviewer. Leonard Cohen simply said, ‘yes’.

​
 

​But if even Leonard Cohen conceded that he made music to get mates I wondered if the sharp distinction we tend to draw between humans with agency and animals without agency is quite so clear-cut.
 
We get pleasure from making music and do this for fun but we do not know why we do it anymore than the birds know why they sing. Do we really have agency? If so where does this come from?

Matosov argued that for a teacher to force children to learn Maths when they do not want to learn Maths is wrong. This is not respecting their agency. People do enjoy Maths, of course, but it does not seem as natural for most children as enjoying making music. It more often seems like a culturally mediated pleasure that people have to be taught first and might learn to enjoy later. In response to this challenge I tried to argue that the issue is not just about the agency of the children but also about the agency of the Maths. Maths is a long-term dialogue bigger than any individual that wants to survive and that can only survive by recruiting individuals. 
 
Why we should teach Maths is also one of the issues addressed in a very practical new book I have co-written with Neil Phillipson. The answer we gave in the book was about the role of education as inducting children into the long term dialogues of culture. The idea is that these long term global dialogues are more powerful in many ways than the short-term and local dialogues that tend to influence whatever it is that children might think that they want to learn right now like how to be a better football player or a pop-star. You cannot really force children to learn what they do not want to learn but you can offer an invitation and help them to engage.
 
Our point was also that participating in these powerful long term dialogues of culture and, more generally, in what Oakeshott has called ‘the conversation of mankind’, is a way for children to become fully human. While some aspects of culture can seem alien to children, humans do not exist apart from culture and it is only by engaging with a culture, internalising it and living it, that we become fully ourselves.
 
Gilbert Simondon argues that we should not look at individuals as if they were fixed and finished final objects but always in terms of the process of individuation that formed them and that continues to form them. His focus on individuation reveals a continuity between nature and culture. Natural processes of individuation, like the way that individual snow-flake crystals precipitate out of the water vapour in a cloud, become doubled in on themselves in biological life: “The living organism conserves within itself a permanent activity of individuation”, he writes in L’individuation psychique et collective. The bird looking for a mate, or just enjoying herself by singing, will produce hundreds of songs each slightly different. In human cultures individuation doubles again. Our thoughts are like the bird song, called out as a response to the world and themselves actions in the world, formations of new patterns of neurons in the brain, or patterns of sounds in the air or ink on the page. But there is a difference. We do not just make music – we ask why. We do not just think, we also reflect on our thinking. Reflective thought is not individual but cultural. By using shared technology such as ink and paper, we are able to exteriorise ourselves and look back as if from other points of view. Humans depend on technology, tools, words, footballs and music recordings, that helps build something collective beyond the biological individual. We could call this culture.  Simondon refers to the trans-individual. Extending Simondon’s quote about the shift from the physical to biological you could characterise the shift from the biological to the cultural in much the same way but up one level: human culture conserves within itself a permanent activity of trans-individuation.

Children’s desires are not fixed in time but evolve as part of a larger never finished  journey of individuation and trans-individuation. Disciplines like Maths might not be what a child want to learn right now but they are part of what a culture wants to learn and cultures learn by co-evolving with biological individuals - sometimes possessing them and sometimes possessed by them. We are never just an individual, never just a culture – but we dance between these two extremes.

Socrates seems to be describing a similar understanding of his role as an educator inducting students into the long-term dialogue of culture when he is reported by Plato in the Phaedrus as saying:

The dialectician chooses a proper soul and plants and sows within it discourse accompanied by knowledge - discourse capable of helping itself as well as the man who planted it, which is not barren but produces a seed from which more discourse grows in the character of others. Such discourse makes the seed forever immortal and renders the man who has it as happy as any human being can be.

Biological individuals have a certain agency, they want to sing, they want to get mates, but, as even Socrates knew, discourses - or trans-individual dialogues - also have agency and they want to survive too and the only way that they can survive and grow is through implanting themselves in biological individuals. Education is motivated by the agency of long-term dialogues. For birds singing for a mate brings joy. For teachers and learners participating in the long-term dialogues of culture brings joy and also the immortality of a trans-individual life.