It is easy to see why dialogue and dialogic teaching could be useful in subjects like literature and history where there are debates between competing points of view and often no certainty as to which one is right. But subjects like maths and science present themselves as essentially monologic, so why should we teach them in a dialogic way?. That 2+2=4 is simply a truth and not a matter for debate. That water boils at 100 degrees C at sea level is a fact not requiring argument and discussion surely? Nonetheless, I think that we do need dialogic education in both maths and science. This short blog explains why.
Last week I gave a talk about dialogic education at a big education conference (EARLI2019 in Aachen). I focussed on how dialogic education can expand awareness by opening up a dialogic space, widening that space by bringing in alternative perspectives and deepening that space by questioning any framing assumptions. Meaning is only possible, I claimed, in the context of dialogue between different perspectives.
The discussant in our symposium, Frank Fisher, said that, while this dialogue approach is obviously useful in citizenship and the humanities it might not apply so well to subjects such as maths and science where there are correct answers to be taught. Frank, a professor at Munich, is a leader in the field of argumentation research. His concern about the limits of dialogic education is probably widely shared.
Anna Sfard, a leader in mathematics education, raises a similar challenge against my account of dialogic education. She quotes me writing that progress in dialogic education is 'not simply from A to B but from A to A + B' and she points out that this does not apply to monologic subjects such as mathematics[i].
This critical challenge from Frank and Anna is really useful in motivating me to express what I mean more clearly and also, perhaps, to think it through a little more carefully - hence this blog.
When I came up with the line that Anna quotes about progress being not from A to B but from A to A + B I was pretty pleased with myself. It expresses the experience of learning by talking to people and seeing the world through their eyes. Each new voice is a new way of seeing that does not replace other voices but augments them. For example, I feel fortunate as an adult that I have not entirely lost the ways of thinking, feeling and seeing the world that I had as a child. In that respect I have not moved simply from A to B (child to adult) but from A to A +B (from child to child plus adult).
But I can see that the idea that learning moves from A to A + B is a big problem if it is taken to mean that you do not just learn that 2+2=4 but also that 2+2=3 and 2+2=5. I see the problem. That does not make any educational sense at all! Let me explain myself with three short examples.
1) Seeing the pattern
With the direct teaching, or the A to B approach, there is a danger that children can apparently learn that 2 + 2 = 4 without understanding what this means. Maybe they can 'count on' 2 fingers from an initial two fingers without understanding why 2+2 is always the same as 1+3 which is always the same as 3+1. To understand that they need to move from the procedural business of 'counting on' to grasp the concept of 'commutativity'.
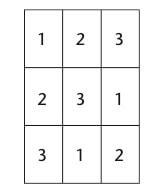
I did some research on this with maths education specialist Carol Murphy by teaching early mathematics in combination with teaching dialogic talk. In one class we observed the children worked together in groups of three solving a simple form of magic square. They were given the numbers 3, 2 and 1 on cards and asked to arrange them in a 3 by 3 grid so that every row and column added up to the same.
Two of the group, Amy and Jack, worked industriously arranging numbers and counting them out while Judy, the third member, just sat to one side and watched them.
‘Two, three and one’ Jack counted on his fingers, ‘that’s six’. ‘One, three and two’, Amy counted on her fingers, ‘six’.
They were succeeding at the task, finding the way in which the numbers could be used to make all the rows and columns add up to the same total but they did not seem to realise that 3 + 2 + 1 was the same as 1 + 2 + 3 and the same as 2 + 1 + 3 etc. Judy sucked her finger looking on then said: ‘They are all adding up to six, look they are all six’. Later the teacher affirmed the point that Judy had made and helped to lead the group away from procedural understanding - knowing how to go on - to conceptual understanding - knowing why. I am not sure how much teaching the ground rules of dialogic talk helped with this small breakthrough but in general dialogue in classrooms has been shown to help with the shift from procedural to conceptual understanding in maths and in science.[2]
2 Three voices are better than one
Working with Neil Mercer in the 1990s I first explored the impact of teaching 'thinking together' (a form of dialogic education) in the context of citizenship. We could show a development in the quality of children's reasoning as a result of teaching Exploratory Talk (a form of dialogic talk) but this effect was hard to measure and quantify. We moved on to using standard non-verbal reasoning tests to measure the impact of dialogic education. We did this precisely because each puzzle had a right answer and so we could easily measure the improvement in problem-solving that resulted from our teaching. As a result of dialogic education many groups moved from getting answers wrong to getting them right. In this respect you could say that they moved from A to B. But our analysis showed that they often achieved this greater success through increasing the complexity of their understanding of the problem. Whereas in the pre-test they often got problems wrong by seeing them only one way, in the post test they often got problems right by seeing them in several different ways and then discussing together which way was best.[3]
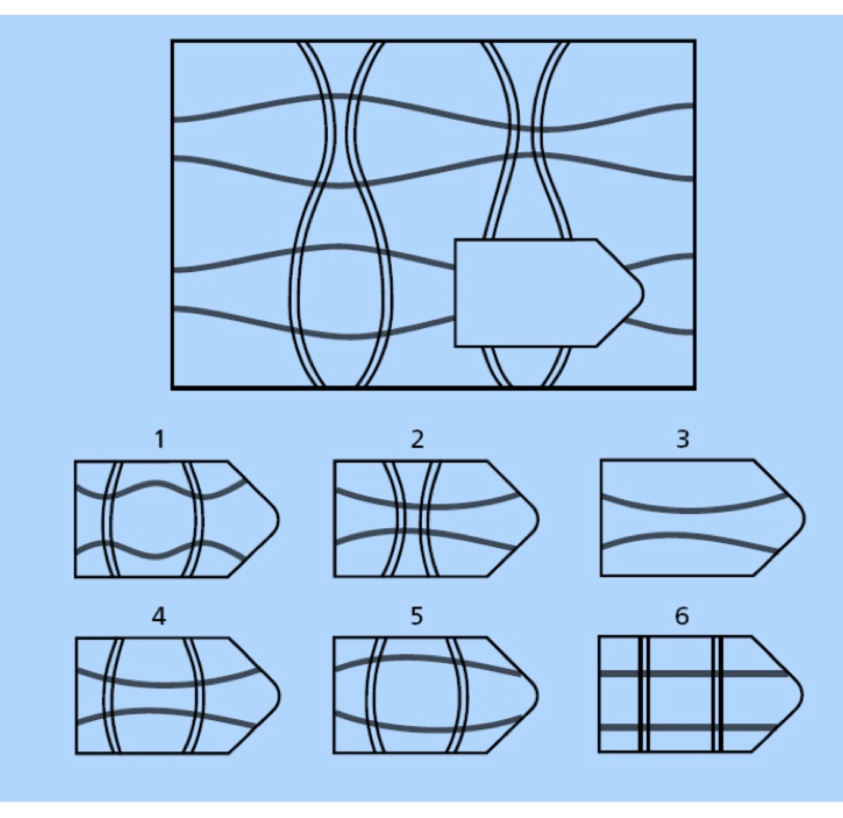
Before the series of Thinking Together lessons one group, Elaine, Danny and John, did not talk together at all well. In the pre-test one person in the group, Elaine, worked out the answer to Problem A (above) alone and wrote it down as number 5. She fell into the trap of just looking at the puzzle from top to bottom. In the post-test we gave this group the same set of puzzles and they got it right. The video recording shows why. As before, it seems that the pattern of the top to bottom lines is noticed first and John offers number five as the answer. But this answer is only made as a suggestion preceded by 'I think'. Danny then put forward number two as the answer, apparently because he is looking at the horizontal pattern of the single lines. John explains (through words and pointing) that the vertical black lines have to ‘go out'. Danny in turn explains that it cannot be number five because the light lines have to ‘go in’. Each of the two boys has adopted a different perspective; John takes the side of the vertical lines, Danny that of the horizontal lines. Each can see enough to refute the position of the other but this does not yet produce the solution. Elaine then comes up with the answer which combines the vertical lines going out with the horizontal lines going in, that is number four. Once she has expressed this both Danny and John agree that she is right, nodding.
There is a single correct answer here which they converge upon. This is monologic. But they only get it because they compare the right answer to the wrong answers. This is dialogic. Understanding the right answer means understanding why it is right which also means understanding the wrong answers in order to contrast and compare.
As a teenager I associated Darwin with the theory that humans had evolved from animals. I was confused when I discovered that lots of other people, Goethe for example, had suggested this same idea long before Darwin had published his 'Origin of Species'. This made me realise that I had not really understood Darwin's theory at all. Darwin had not only speculated on man evolving from animals but had offered a theory as to the mechanism whereby evolution worked. This mechanism is variation of organisms combined with selection by survival and reproduction. I really understood this more specific theory only when I saw Darwin's theory of evolution compared with Lamarck’s theory. Lamarck’s theory is just as much a theory of evolution as Darwin's but it did not work as well to explain the available evidence. This theory is that organisms strive to adapt to their environment in their lifetimes and then passed on this adaptation on to their offspring. Giraffes that stretched to reach leaves in high trees grew longer necks and so their children inherited these longer necks.
Understanding the debate in the 19th century between these contrasting views of evolution helped me to understand what was special about Darwin's theory. It is also interesting that, although Lamarck’s view was 'defeated' at the time it has returned. Recent evidence has demonstrated that features acquired through experience in a lifetime can in fact be transmitted to offspring and so Lamarck's name is being referenced in biology articles once again [4].
My point is that, as with Mathematics, to understand a theory in science, it is not enough to just state it - it does not mean anything on its own outside of any dialogic context - it means something in relation to the dialogue that spawned it and the ongoing dialogues that it is engaged within. To understand it then is also to understand the apparently 'wrong' theories that it contrasts with. But even these wrong theories do not really disappear from the dialogue - they remain around as resources to help us think and so to help us to be able to respond to new challenges.
It is true that some difference in pedagogy is required if the objective is for students to end up knowing a correct way as opposed to if the objective is to explore the range of ways. However, these different objectives and associated pedagogies can both be valued and combined in any subject area [5]. There can be convergence on a single truth in history and literature just as there can be discussion of a range of perspectives in maths and science. Arguing that progress is expansive and moves not simply from A to B but from understanding only A to understanding both A and B is not meant to suggest that all points of view are equally valid. It is meant to suggest that understanding why one way is better than another (in a context) requires understanding the contrasting views and so requires mastering a dialogic space [6].
[1] Sfard, A (in press for 2019) Learning, discursive faultiness and dialogic engagement. In Mercer, Wegerif and Major (eds) The Routledge international handbook of research on dialogic education.
[2] Wegerif, R. (2010) Mindexpanding. McGraw Hill
[3] Wegerif, R., Mercer, N., & Dawes, L. (1999). From social interaction to individual reasoning: An empirical investigation of a possible socio-cultural model of cognitive development. Learning and instruction, 9(6), 493-516.
[4] West-Eberhard, M. J. (2007). Dancing with DNA and flirting with the ghost of Lamarck. Biology and Philosophy, 22(3), 439-451.
[5] Scott, P. H., Mortimer, E. F., & Aguiar, O. G. (2006). The tension between authoritative and dialogic discourse: A fundamental characteristic of meaning making interactions in high school science lessons. Science education, 90(4), 605-631.
[6] Phillipson, N., & Wegerif, R. (2016). Dialogic Education: Mastering core concepts through thinking together. Routledge.

 RSS Feed
RSS Feed